Números como π, e e φ geralmente aparecem em lugares inesperados na ciência e na matemática. O triângulo de Pascal e a sequência de Fibonacci também parecem inexplicavelmente difundidos na natureza. Depois, há a função zeta de Riemann, uma função enganosamente direta que tem deixado os matemáticos perplexos desde o século 19. O dilema mais famoso, a hipótese de Riemann, é talvez a maior questão não resolvida da matemática, com o Clay Mathematics Institute oferecendo um prêmio de US$ 1 milhão por uma prova correta.
O físico da UC Santa Barbara, Grant Remmen, acredita ter uma nova abordagem para explorar as peculiaridades da função zeta. Ele encontrou um análogo que traduz muitas das propriedades importantes da função na teoria quântica de campos. Isso significa que os pesquisadores agora podem aproveitar as ferramentas desse campo da física para investigar a enigmática e estranhamente onipresente função zeta. Seu trabalho poderia até levar a uma prova da hipótese de Riemann. Remmen expõe sua abordagem na revistaPhysical Review Letters.
“A função zeta de Riemann é essa função matemática famosa e misteriosa que surge na teoria dos números em todo o lugar”, disse Remmen, um estudioso de pós-doutorado no Kavli Institute for Theoretical Physics da UCSB. “Tem sido estudado por mais de 150 anos.”
Uma perspectiva externa
Remmen geralmente não trabalha em resolver as maiores questões da matemática. Ele geralmente está preocupado em resolver as maiores questões da física. Como bolsista de física fundamental da UC Santa Barbara, ele normalmente dedica sua atenção a tópicos como física de partículas, gravidade quântica, teoria das cordas e buracos negros. “Na moderna teoria de alta energia, a física das maiores e menores escalas guardam os mistérios mais profundos”, observou ele.
Uma de suas especialidades é a teoria quântica de campos, que ele descreve como um “triunfo da física do século 20”. A maioria das pessoas já ouviu falar da mecânica quântica (partículas subatômicas, incerteza, etc.) e da relatividade especial (dilatação do tempo, E=mc2 e assim por diante). “Mas com a teoria quântica de campos, os físicos descobriram como combinar a relatividade especial e a mecânica quântica em uma descrição de como as partículas se movem na velocidade da luz ou perto dela”, explicou ele.
A teoria quântica de campos não é exatamente uma teoria única. É mais como uma coleção de ferramentas que os cientistas podem usar para descrever qualquer conjunto de interações de partículas.
Remmen percebeu que um dos conceitos compartilha muitas características com a função zeta de Riemann. É chamado de amplitude de espalhamento e codifica a probabilidade da mecânica quântica de que as partículas irão interagir umas com as outras. Ele ficou intrigado.
As amplitudes de espalhamento geralmente funcionam bem com momentos que são números complexos. Esses números consistem em uma parte real e uma parte imaginária – um múltiplo de √-1, que os matemáticos chamam de i. As amplitudes de espalhamento têm boas propriedades no plano complexo. Por um lado, eles são analíticos (podem ser expressos como uma série) em torno de todos os pontos, exceto um conjunto selecionado de pólos, que estão todos ao longo de uma linha.
“Isso parecia semelhante ao que está acontecendo com os zeros da função zeta de Riemann, que parecem estar em uma linha”, disse Remmen. “E então pensei em como determinar se essa aparente semelhança era algo real.”
Os pólos de amplitude de espalhamento correspondem à produção de partículas, onde ocorre um evento físico que gera uma partícula com momento. O valor de cada pólo corresponde à massa da partícula que é criada. Portanto, tratava-se de encontrar uma função que se comportasse como uma amplitude de espalhamento e cujos polos correspondessem aos zeros não triviais da função zeta.
Com caneta, papel e um computador para verificar seus resultados, Remmen começou a trabalhar na concepção de uma função que tinha todas as propriedades relevantes. “Eu tive a ideia de conectar a função zeta de Riemann às amplitudes no fundo da minha mente por alguns anos”, disse ele. “Uma vez que comecei a encontrar tal função, levei cerca de uma semana para construí-la, e explorar completamente suas propriedades e escrever o artigo levou alguns meses.”
Enganosamente simples
Em seu núcleo, a função zeta generaliza a série harmônica:
Epifania quântica zeta: físico encontra uma nova abordagem para um enigma matemático de US $ 1 milhão
Esta série vai até o infinito quando x ≤ 1, mas converge para um número real para cada x > 1.
Em 1859 Bernhard Riemann decidiu considerar o que aconteceria quando x é um número complexo. A função, agora com o nome Riemann zeta, recebe um número complexo e cospe outro.
Riemann também decidiu estender a função zeta para números onde a componente real não era maior que 1, definindo-a em duas partes: a definição familiar vale nos lugares onde a função se comporta, e outra definição implícita cobre os lugares onde normalmente explodiria até o infinito.
Graças a um teorema em análise complexa, os matemáticos sabem que há apenas uma formulação para esta nova área que preserva suavemente as propriedades da função original. Infelizmente, ninguém conseguiu representá-lo de uma forma com um número finito de termos, o que faz parte do mistério que envolve essa função.
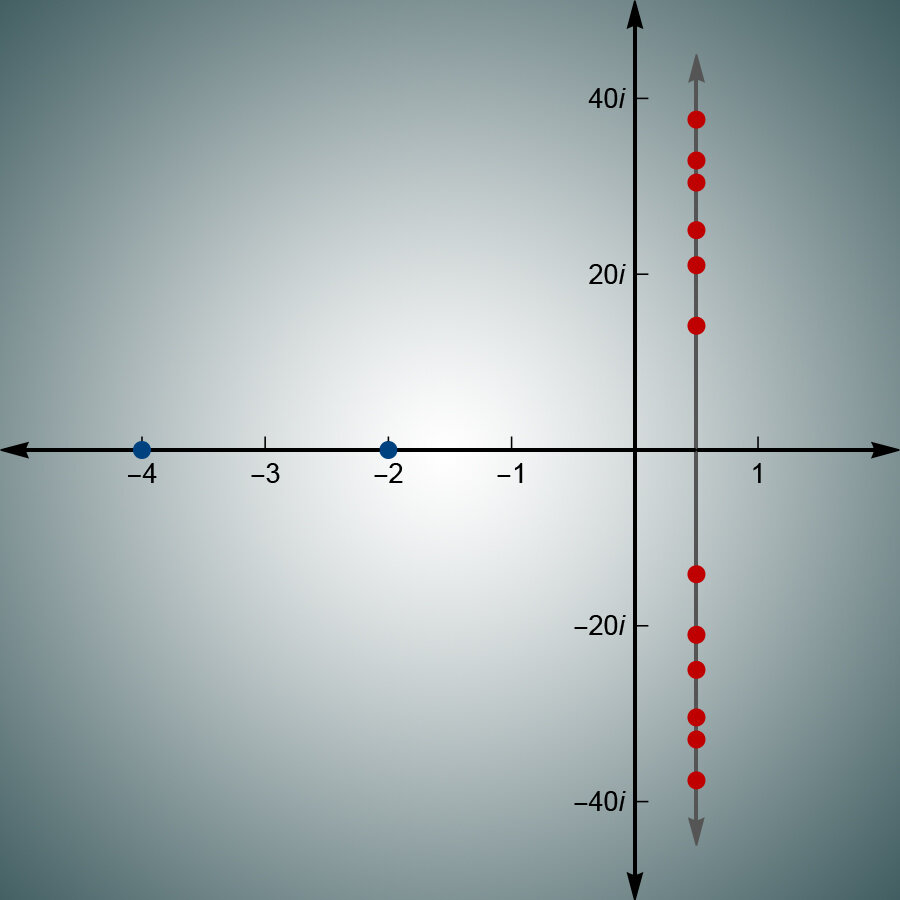
Dada a simplicidade da função, ela deve ter alguns recursos interessantes. “E, no entanto, essas propriedades acabam sendo terrivelmente complicadas de entender”, disse Remmen. Por exemplo, pegue as entradas onde a função é igual a zero. Todos os números pares negativos são mapeados para zero, embora isso seja aparente – ou “trivial”, como dizem os matemáticos – quando a função zeta é escrita em certas formas. O que deixou os matemáticos perplexos é que todos os outros zeros não triviais parecem estar ao longo de uma linha: cada um deles tem um componente real de ½.
Riemann levantou a hipótese de que esse padrão vale para todos esses zeros não triviais, e a tendência foi confirmada para os primeiros trilhões deles. Dito isto, há conjecturas que funcionam para trilhões de exemplos e depois falham em números extremamente grandes. Portanto, os matemáticos não podem ter certeza de que a hipótese é verdadeira até que seja provada.
Mas se for verdade, a hipótese de Riemann tem implicações de longo alcance. “Por várias razões, surge em todo lugar em questões fundamentais em matemática”, disse Remmen. Postulados em campos tão distintos quanto a teoria da computação, a álgebra abstrata e a teoria dos números dependem da hipótese que se mantém verdadeira. Por exemplo, prová-lo forneceria um relato preciso da distribuição de números primos.
Um análogo físico
A amplitude de dispersão que Remmen encontrou descreve duas partículas sem massa interagindo trocando um conjunto infinito de partículas massivas, uma de cada vez. A função tem um pólo – um ponto onde não pode ser expresso como uma série – correspondente à massa de cada partícula intermediária. Juntos, os pólos infinitos se alinham com os zeros não triviais da função zeta de Riemann.
O que Remmen construiu é o principal componente da interação. Há infinitamente mais que cada um responde por aspectos cada vez menores da interação, descrevendo processos que envolvem a troca de várias partículas massivas de uma só vez. Essas “amplitudes em nível de loop” seriam objeto de trabalhos futuros.
A hipótese de Riemann postula que todos os zeros não triviais da função zeta têm um componente real de ½. Traduzindo isso para o modelo de Remmen: Todos os pólos da amplitude são números reais. Isso significa que, se alguém puder provar que sua função descreve uma teoria quântica de campo consistente – ou seja, uma em que as massas são números reais, não imaginários -, a hipótese de Riemann será comprovada.
Essa formulação traz a hipótese de Riemann para mais um campo da ciência e da matemática, com ferramentas poderosas para oferecer aos matemáticos. “Não há apenas essa relação com a hipótese de Riemann, mas há toda uma lista de outros atributos da função zeta de Riemann que correspondem a algo físico na amplitude de espalhamento”, disse Remmen. Por exemplo, ele já descobriu identidades matemáticas não intuitivas relacionadas à função zeta usando métodos da física.
O trabalho de Remmen segue uma tradição de pesquisadores que procuram a física para esclarecer os dilemas matemáticos. Por exemplo, o físico Gabriele Veneziano fez uma pergunta semelhante em 1968: se a função beta de Euler poderia ser interpretada como uma amplitude de espalhamento. “De fato pode”, observou Remmen, “e a amplitude que Veneziano construiu foi uma das primeiras amplitudes da teoria das cordas.”
Remmen espera aproveitar essa amplitude para aprender mais sobre a função zeta. “O fato de que existem todos esses análogos significa que há algo acontecendo aqui”, disse ele.
E a abordagem abre um caminho para possivelmente provar a hipótese secular. “As inovações necessárias para provar que essa amplitude vem de uma teoria de campo quântica legítima daria, automaticamente, as ferramentas necessárias para entender completamente a função zeta”, disse Remmen. “E provavelmente lhe daria mais também.”
Achou útil essa informação? Compartilhe com seus amigos! ?
Deixe-nos a sua opinião aqui nos comentários.