O Teorema de Pitágoras mudou. Melhor ainda, nossa compreensão dele mudou – de duas a três dimensões. Durante os últimos 2.500 anos, o Teorema de Pitágoras sem dúvida, é o teorema mais conhecido no mundo e tem ajudado muito a humanidade a se evoluir. Seus ângulos retos estão por toda a parte, em um edifício, numa tabela, num gráfico com eixos ou na estrutura atômica de um cristal. É aplicável universalmente, mas ainda está exclusivamente ligado a duas dimensões.
Bem, o que faz com que pareça em 3D?
Até agora, isto não era conhecido. Nos últimos 5 anos, o engenheiro aeronáutico e espacial Luis Teia trabalho sobre o tema. Na sequência do seu recente artigo, chamado de Pythagoras triples explained via central squares, publicado na edição de 2015 no Australian Senior Mathematics Journal, ele derivou a demonstração.
Vamos explicar brevemente o que isso significa.
Enquanto a demonstração 2D do Teorema de Pitágoras é desenhado a mão e coube em meia página, a versão tridimensional exige um livro com 120 páginas. O que é muito complexo! A parte geométrica foi tirada usando o CAD, e a álgebra da matemática abrange 2/3 do livro. Notavelmente, tanto a demonstração 2D e 3D do Teorema de Pitágoras estão interligados. Além disso, a versão 3D é construída a partir da 2D de forma única.
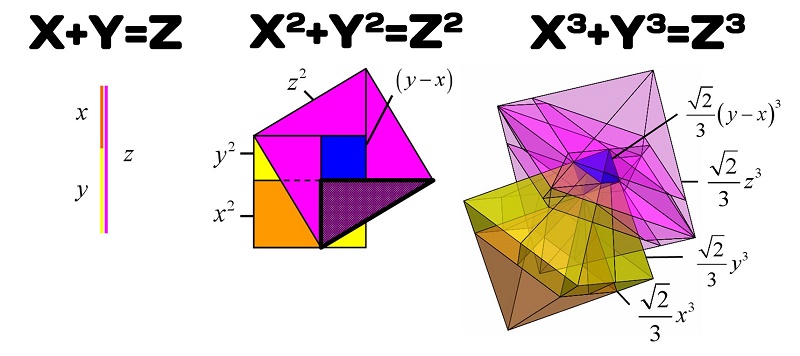
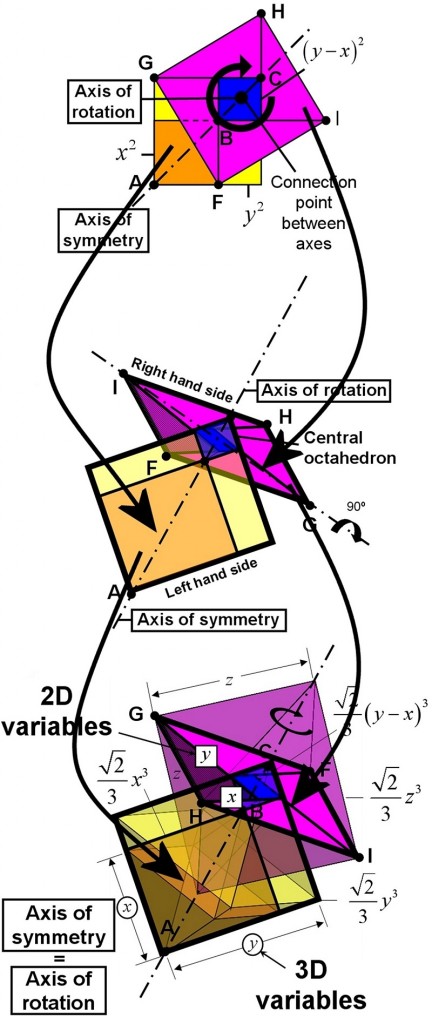
O lado direito do teorema é girado em 90 graus. O quadrado azul se transforma em um octaedro azul – o equivalente tridimensional de um quadrado. Isto significa que a medida que o teorema 2D é construído a partir de quadrados, o 3D é construído a partir de octaedros. Consequentemente, pode-se encontrar o teorema 2D dentro do 3D ao notar a presença do triângulo de ângulo reto à sombra. As implicações podem ser tomadas num nível mais profundo por perceber que as novas variáveis 3D são regidas pela 2D. Explicações detalhadas podem ser encontradas no livro do Engenheiro Luis Teia, ”X3 + Y3 = Z3: A Demonstração”, ou ”X3+Y3=Z3: The Proof”.
Por que isso é importante?
Considerando o salto tecnológico radical que Pitágoras trouxe para a humanidade com seu teorema cerca de 2,5 mil anos atrás, as implicações desta nova versão 3D pode ser igualmente significativa. Talvez, isso leva a uma versão dimensional “atualizada” da nossa trigonometria atual. Quanto à próxima meta do engenheiro Luis Teia será explorar a demonstração do teorema de Fermat usando esta nova abordagem. Quem sabe?
Achou útil essa informação? Compartilhe com seus amigos! xD
Deixe-nos a sua opinião aqui nos comentários.