O matemático Ian Stewart publicou o livro “Dezessete equações que mudaram o mundo”. São equações que, ao longo do tempo, moldaram nossa compreensão do universo de inúmeras maneiras.
9 equações que mudaram o curso da história – Parte II
Você vai conhecê-las agora:
Teorema de Pitágoras (Pitágoras, 530 aC)
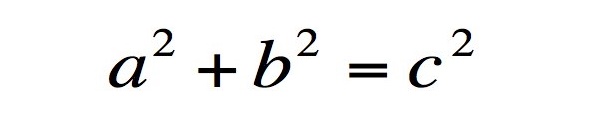
É um teorema fundamental para a nossa compreensão a respeito da geometria. Ele descreve a relação entre os lados de um triângulo retângulo em uma superfície plana: a soma das áreas dos quadrados construídos sobre os catetos (a e b) equivale à área do quadrado construído sobre a hipotenusa (c). 🙂
Logaritmos (John Napier, 1610)
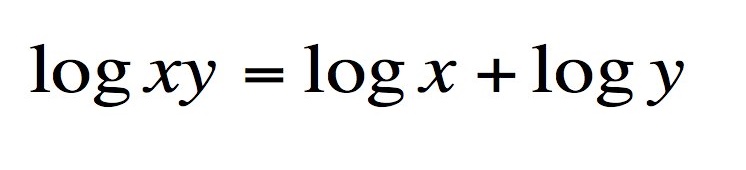
Logaritmos são os opostos das funções exponenciais. O logaritmo de um número é o expoente a que outro valor fixo, a base, deve ser elevado para então obter este número. Por exemplo, o logaritmo de 1000 na base 10 é 3 porque 10 ao cubo é 1000 (1000 = 10 × 10 × 10 = 10³).
A equação que você viu logo acima, mostra uma das aplicações mais úteis de logaritmos: transformar uma multiplicação em uma adição. Até o desenvolvimento do computador digital, esta era a alternativa mais comum de se multiplicar rapidamente um grande número, acelerando o tempo de importantes cálculos da física, astronomia e claro, engenharia.
Cálculo (Isaac Newton, 1668)
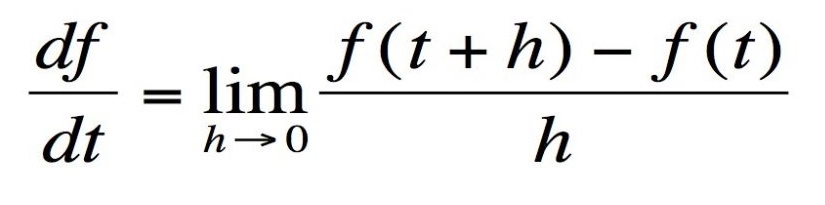
O que você viu acima é a função derivada no cálculo. Ela mede a taxa na qual uma quantidade está mudando. Vamos citar um exemplo, podemos pensar na velocidade como sendo derivada da posição – se você estiver andando 1 km por hora, em seguida, a cada hora, você altera a sua posição por 1 km.
Grande parte da ciência está interessada em compreender como é que as coisas mudam, e a derivada e também a integral – outro fundamento do cálculo – é como os matemáticos e cientistas compreendem tais mudanças.
Lei da Gravidade (Isaac Newton, 1687)
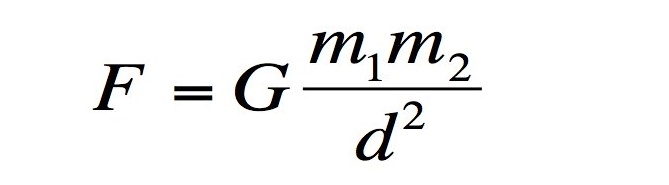
A Lei da Gravidade de Newton descreve a força da gravidade entre dois objetos, designado F, em termos de uma constante universal, chamado G, das massas dos dois objetos, m1 e m2, e da distância entre os objetos, d.
A lei é uma parte notável da história científica, isto é, explica, quase que perfeitamente por que os planetas se movem da maneira que se movem. Também notável é a sua natureza universal, o que quer dizer que não funciona só para a gravidade na Terra, ou no sistema solar, mas em qualquer lugar do universo.
Raiz quadrada de -1 (Leonhard Euler, 1750)
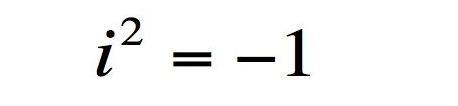
A raiz quadrada de -1 dá origem aos números complexos.
Álgebra funciona perfeitamente do jeito que queremos, ou seja, qualquer equação que tem uma solução em número complexo, uma situação que não é verdade para números reais: x + 4 = 0 não tem solução com número real, mas tem uma solução complexa, a raiz quadrada de -4 ou então 2i.
Cálculo, por sua vez pode ser estendido para os números complexos e, quando fazemos isso, encontramos simetrias e propriedades surpreendentes dois tais números. Essas propriedades tornam os números complexos essenciais em eletrônica e também em processamento de sinais.
Relação de Euler (Leonhard Euler, 1751)
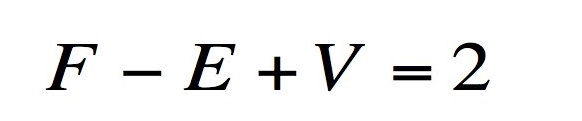
Poliedros são nada mais que as versões tridimensionais de polígonos. Os cantos de um poliedro são chamados de vértices, as linhas que ligam os vértices são chamadas de arestas, e os polígonos são as faces.
Um cubo tem 8 vértices, 12 arestas e 6 faces. Na equação temos: 8 + 6 – 12 = 2. A fórmula de Euler diz que, desde que o poliedro seja não tenha vícios, se você adicionar suas vértices e faces e subtrair as arestas, sempre terá como resultado 2. Isto será verdadeiro se o seu poliedro tem 4, 8, 12, 20 ou qualquer outro número de faces.
Esta relação abriu o caminho para o desenvolvimento da topologia, um ramo da matemática essencial para a física moderna.
Distribuição normal (Carl Friedrich Gauss, 1810)
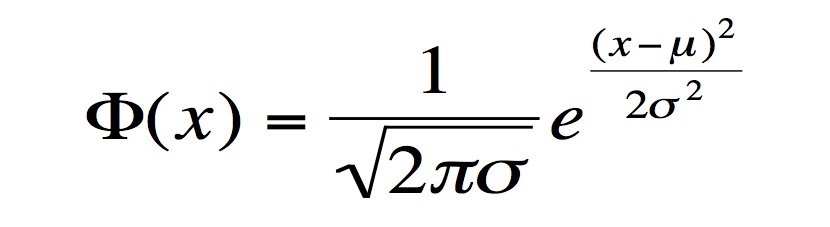
A distribuição normal ou também distribuição de Gauss está presente na estatística. Essa curva é usada em física, biologia e ciências sociais para modelar várias propriedades.
Uma das quais as razões da distribuição normal aparecer muitas vezes é que ela descreve o comportamento de grandes grupos de processos independentes.
Equação da onda (Jean le Rond d’Alembert, 1746)
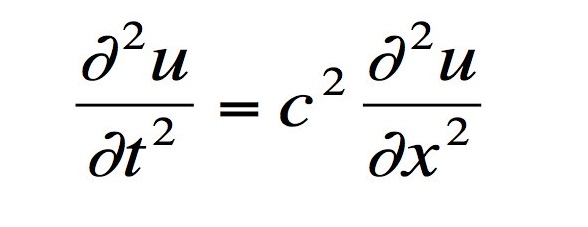
É uma equação diferencial parcial linear, e que descreve o comportamento das ondas (tanto sonoras, quanto aquáticas, luminosas, como uma corda de violão vibrando, ondulações em uma lagoa após uma pedra ser jogada na água, ou a luz proveniente de uma lâmpada incandescente). UFA!!!
As técnicas que são desenvolvidas para resolver a equação abriram as portas para a compreensão de outras equações diferenciais também.
9 equações que mudaram o curso da história – Parte II
Achou útil essa informação? Compartilhe com seus amigos! xD
Deixe-nos a sua opinião aqui nos comentários.