O Matemático Ian Stewart publicou o livro “Dezessete equações que mudaram o mundo”. São equações que, ao longo do tempo, moldaram nossa compreensão do universo de inúmeras maneiras.
8 equações que mudaram o curso da história – Parte I
Você vai conhecê-las agora:
Transformada de Fourier (Jean-Baptiste Joseph Fourier, 1822)
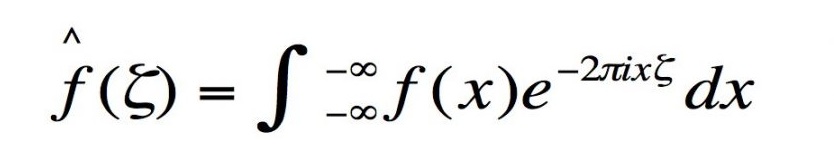
Esta transformada é fundamental para entender as estruturas de onda mais complexas, como a fala humana, por exemplo. Dada uma função de onda complicada, como uma gravação de uma pessoa falando, a transformada permite quebrar esta função em uma combinação de uma série de ondas simples, facilitando assim a sua análise.
A transformada de Fourier é o cerne da transformação moderna e da análise de sinais e compressão de dados. Muito presente em engenharia elétrica com ênfase em telecomunicações, curso na qual sou acadêmico.
Equações de Navier-Stokes (C. Navier e G. Stokes, 1845)
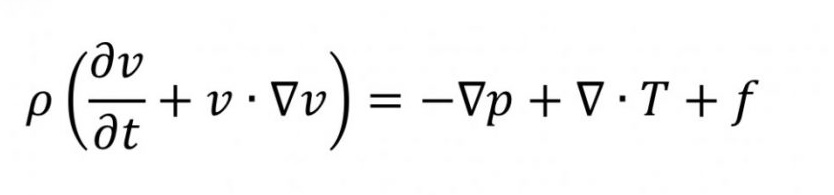
São equações diferenciais. Elas descrevem o comportamento de fluidos, como a água em movimento através de um tubo, o fluxo de ar sobre uma asa de avião, ou até mesmo fumaça de um cigarro.
Equações de Maxwell (James Clerk Maxwell, 1865)
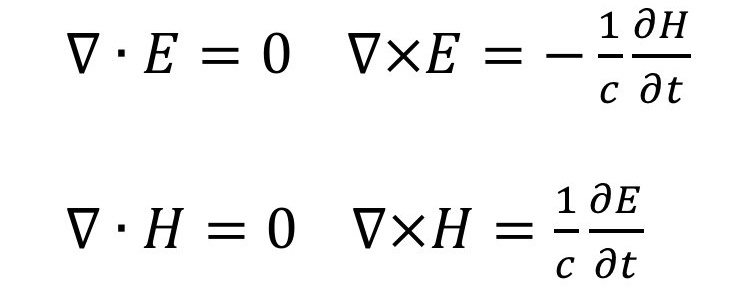
As quatro equações diferenciais acima descrevem o comportamento e relacionamento entre a eletricidade e magnetismo. Elas são a base da nossa explicação de como funciona o eletromagnetismo no nosso dia a dia.
Para tando, a física moderna se baseia em uma explicação da mecânica quântica do eletromagnetismo. Essas equações, no entanto, são apenas uma aproximação que funciona bem em escalas humanas.
Segunda Lei da Termodinâmica (Ludwig Boltzmann, 1874)
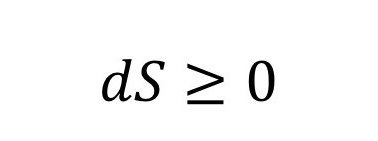
O que você vê acima é a definição de um sistema fechado, a entropia no sistema é sempre constante ou crescente. A entropia termodinâmica é, para ilustrar de forma simples, uma medida de quão desordenado um sistema é. Um sistema que começa em um estado desigual – por exemplo, uma região quente ao lado de uma região fria – sempre tende a se equilibrar, com o calor fluindo da área quente para a área fria até ficar a temperatura ficar em equilíbrio.
A segunda lei da termodinâmica é um dos poucos casos na física onde o tempo realmente importa. A maioria dos processos físicos são no entanto reversíveis. Essa lei só funciona em um sentido. Se colocarmos um cubo de gelo em um copo com café quente, ele sempre vai derreter. O café nunca vai congelar.
Teoria da relatividade (Albert Einstein, 1905)
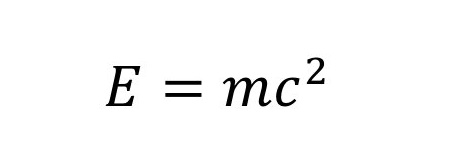
Einstein alterou radicalmente o curso da física com suas teorias da relatividade. A equação clássica E = mc² diz que matéria e energia são equivalentes entre si.
A relatividade geral foi a primeira grande mudança importante na nossa compreensão da gravidade desde a lei de Newton. Ela é essencial para a nossa compreensão das origens, estrutura e destino final do universo.
Equação de Schrodinger (Erwin Schrödinger, 1927)
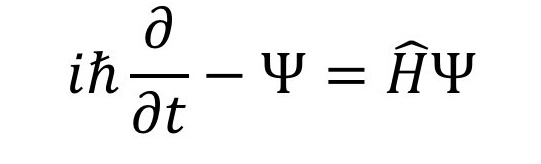
É a principal equação da mecânica quântica. Esta equação governa o comportamento dos átomos e partículas subatômicas.
A mecânica quântica moderna e a relatividade geral são as duas teorias científicas mais bem sucedidas da história – todas as observações experimentais que fizemos até à data de hoje são inteiramente consistentes com tais previsões. A mecânica quântica também é necessária para a maioria da tecnologia moderna – de energia nuclear a computadores baseados em semicondutores e também lasers, todos são construídos em torno de fenômenos quânticos.
Teoria da informação (Claude Shannon, 1949)
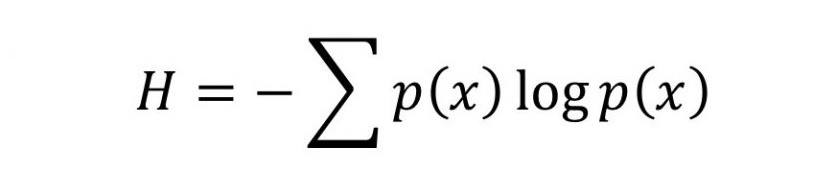
A equação acima serve para obter informações da medida de entropia de Shannon. Tal como acontece com a entropia termodinâmica, esta é uma medida de desordem. Neste caso, mede o conteúdo de informação de uma mensagem, como por exemplos; livros, uma imagem JPEG enviada pela internet, ou qualquer coisa que pode ser representada simbolicamente. Ela representa um limite inferior de quanto essa mensagem pode ser comprimida sem perder parte de seu conteúdo ou qualidade.
A medida de entropia de Shannon lançou o estudo matemático da informação, e seus resultados são cruciais para a forma como nos comunicamos através de redes hoje.
Teoria do caos (Robert May, 1975)
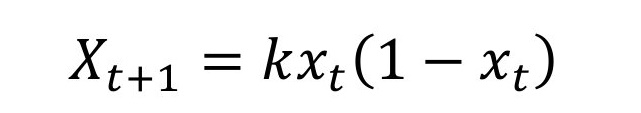
Ela define o mapa logístico de May. Descreve um processo de evolução ao longo do tempo. O “k” é uma constante qualquer. Para certos valores de k, o mapa mostra comportamento caótico: se começarmos em algum valor particular para x, o processo irá evoluir de uma maneira, mas se começarmos com outro valor, mesmo muitos, mas muito parecido com o primeiro valor, o processo irá evoluir de uma maneira completamente diferente. Surpreendente, não?
Vemos comportamento caótico, sensível às condições iniciais, como este em muitas áreas. O clima é um exemplo clássico. Tal conceito é comumente capturada no famoso conceito de uma borboleta batendo suas asas em um continente e causando um furacão em outro continente.
Modelo Black-Scholes (F. Black e M. Scholes, 1990)
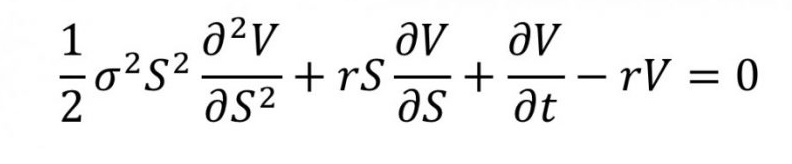
Mais uma equação diferencial, o modelo Black-Scholes descreve como especialistas em finanças e comerciantes determinam preços para derivados. Derivados – são produtos financeiros com base em algum ativo subjacente, por exemplo, uma ação – são uma parte importante do sistema financeiro moderno.
A equação de Black-Scholes permite que profissionais calculem o valor destes produtos financeiros, com base nas propriedades do derivado e do ativo subjacente.
8 equações que mudaram o curso da história – Parte I
Achou útil essa informação? Compartilhe com seus amigos! xD
Deixe-nos a sua opinião aqui nos comentários.


